The term encryption refers to a process of taking a message and “scrambling” its contents so that only the intended person can decrypt the ciphertext (encrypted message). In cryptography, there are two types of encryption:
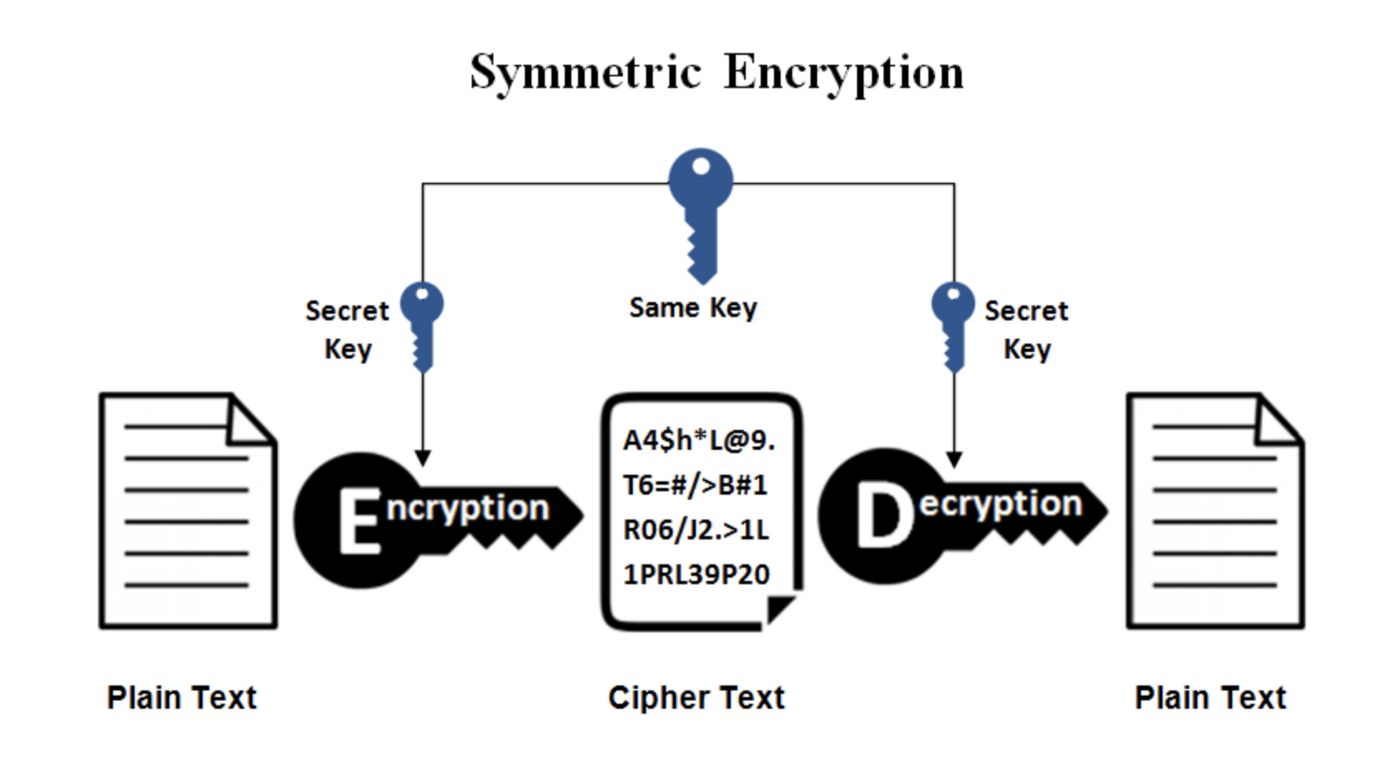
- Symmetric encryption
This is the simplest type of encryption that involves a single key that both encrypts AND decrypts ciphertext. e.g. Blowfish, AES, RC4, DES, RC5, RC6, etc. The most widely used symmetric algorithm is AES-128, AES-192, and AES-256.
- Asymmetric encryption (Public-Key Cryptography)
This is a method which the key to encrypt the plaintext (original message) is distinguished from the key to decrypt the ciphertext. A public key is used to encrypt the plaintext, while a private key is used to decrypt the ciphertext. e.g. RSA, DSA, Elliptic Curve DSA, PKCS, etc.

Up until the 1970s, cryptography had been based on symmetric keys- that is, the sender encrypts their message using a specific key and the receiver decrypts the message using an identical key.
For Alice and Bob to communicate securely with symmetric encryption method, they must share identical keys. However, establishing a shared key is often impossible if Alice when Bob cannot physically meet or requires extra communications overhead.
In 1977, three mathematicians named Rivest, Shamir, and Adleman, developed the RSA encryption method which became one of the most powerful and secure algorithm today. Main characteristics of RSA is that it doesn’t require key to be exchanged between parties; the basic idea behind RSA is that it uses large prime numbers to generate a pair of keys– 1 public key and 1 private key.
In this article, we will look at how the key pairs are mathematically derived with application of RSA algorithm.
0. Assumption
The security strength of RSA algorithm is based on an assumption that factoring a large number into product of prime numbers* is very difficult and time-consuming. For example, if we have two prime numbers 89 and 71, we can easily compute that the product of the two numbers is 6,319. However, it would not be easy if you are given 6,319 and were asked to factor this number into product of prime numbers. (Of course, computers are able to solve our example above within milliseconds)
*Definition 1) We say that a positive integer x > 1 is a prime number if the complete set of divisors of x is 1 and itself. (e.g. 2, 3, 5, 7, ….)
1. Select a random set of prime numbers p and q such that p ≠ q
In this example, we will use $p = 11,\ q = 17$ for convenience.
(Note that in real life, one should use a very large prime number to ensure security of the encrypted message)
2. Calculate n = p x q
n = 11 * 17 = 187
3. Calculate Φ(n) = (p-1)(q-1)
Definition 2) Φ(n), also known as Euler’s totient function, is the number of positive integers less than n that are relatively prime to n.
Definition 3) Two integers a and b are said to be relatively prime (coprime) if gcd(a,b) = 1.
So we have: Φ(n) = Φ(187) = (11-1)(17-1) = 160
4. Select integer e such that gcd(Φ(n), e) = 1, where 1 < e < Φ(n)
We want e such that gcd(160, e) = 1.
Let’s choose e = 7 and see if gcd(160, 7)= 1:
160 = (2^5) * 5
Since 7 is prime and 7 does not divide 160, we know 7 and 160 are relatively prime.
5. Solve for d such that d*e modΦ(n) ≡ 1
We want a number d such that 7*d mod 160 = 1; i.e., we want to find the modular inverse of e with respect to Φ(n).
To do so, we use the extended Euclidean algorithm to solve our equation.
160x + 7y = 1
⇔ 160 = 7(22) + 6
⇔ 7 = 6(1) + 1
Now we perform backward substitution to express 1 as a linear combination of 7 and 160:
1 = 7 – 6(1)
⇔ 7 – (160 – 7(22))
⇔ 7(23) – 160(1)
⇔ 7(23) + 160(-1)
⇒ x = -1, y = 23.
⇒ 160(-1) + 7(23) = 1.
Therefore, we have d ≡ 23 mod 160.
Since 23 ≡ 23 mod 160, we will choose d = 23 for convenience.
* For detailed explanation on modular arithmetic and Euclidean algorithm, check out following links:
6. Find public key and private key
So far, we have all the values needed to generate the public key and private key.
p = 11, q = 17
n = 187
Φ(n) = 160
e = 7
d = 23
∴ Public key = KU = {e, n} = {7, 187}
∴ Private Key = KR = {d, n} = {23, 187}
Now that we have generated the key pairs using the RSA algorithm, we will try encrypting and decrypting using our key pairs.
Encryption
Suppose Alice wants to send a plaintext message M (where M < n) to Bob.
Let M = 8.
Then, the ciphertext of M is:
C ≡ (M^e) mod n
≡ (8^7) mod 187
≡ [{(8^3)^2} * 8] mod 187
≡ {(512^2) * 8} mod 187
≡ [{(-49)^2} * 8] mod 187
≡ 2401*8 mod 187
≡ -30*8 mod 187
≡ -240 mod 187
≡ 134 mod 187
∴ Ciphertext of M=8 is C ≡ 134 (mod 187)
Decryption
Now that Alice sent the ciphertext C=134 to Bob, Bob wants to decrypt the message using his private key d = 23.
Given C, we can decrypt the ciphertext into plaintext M with the following procedure:
M ≡ C^d mod n
≡ 134^23 mod 187
Using a calculator, we get
M ≡ 8 (mod 187), which is the correct plaintext.
To summarize, the RSA algorithm procedure is as follows:
Key Generation
- Select two prime numbers, p and q
- Calculate n = pq
- Calculate Φ(n) = (p-1)(q-1)
- Select integer e such that gcd(Φ(n), e) = 1 where 1 < e < Φ(n)
- Solve for d such that d*e modΦ(n) ≡ 1 ∴ Public Key: KU = {e, n} ∴ Private Key: KR = {d, n}
Encryption
Plaintext: M < n
Ciphertext: C = (M^e)(mod n)
Decryption
Ciphertext: C
Plaintext: M = (C^d)(mod n)